Can energy be produced without combustion?
Magneto Thermodynamics
The fine art of demonology,
by Steven J. SmithPart 1
1.1.1
Introduction:
Can energy be produced without combustion? A simple question, the answer to which, has profound consequences for the future of mankind (under the term "combustion", I include both nuclear fission and fusion, as well as the more conventional forms of combustion). Owing to the controversy surrounding this subject, rather than simply diving into the math and physics, I will take the unusual step of prefacing my paper with a discussion of the historical and societal underpinnings of this debate. In part 2, we shall build a solid scientific foundation for the existence of anti-entropic devices, and in part 3 we shall apply these principals to inductive kickback generators such as the Tesla and Hendershot devices.
1.1.2
The Man:
In the 19th century, James C. Maxwell, a British scientist, formulated his now famous set of 4 equations, the first complete description of electromagnetic interactions. For this contribution, he is celebrated in physics and history books around the world. This same gentleman also gave science a daemon. And since the dawn of the 20th century, scientists the world over have, almost without exception, vehemently denied the very existence of Maxwell's Daemon. These denials were not based on any experiment intended to discover the existence (or lack) of the daemon. Instead the scientists relied on circular logic, claiming the daemon could not exist, because it's existence would violate the very law of physics Maxwell hypothesized his daemon could circumvent.
1.1.3
The Daemon:
For those who have little or no knowledge of Maxwell and his daemon, we'll start with a simple explanation of how the daemon works. Imagine a container filled with air, and divided by a thin partition into two separate compartments (A & B). There is a small hole in the partition, and an equally small trap door covering the hole. The hole is just large enough, that when the door is opened, single air molecules can move through the hole, thereby passing from one compartment, into the other. Now suppose we have a tiny intelligent being (the daemon) who opens and closes the door, based on a simple set of rules:
Over time, compartment B will accumulate a majority of fast moving air molecules, and compartment A will accumulate a majority of slow moving air molecules. In thermodynamic terms, compartment B will become hotter, and compartment A will become colder. In other words, through the actions of the daemon, a temperature difference will arise, where none existed before. It would seem that Maxwell's daemon has just broken the second law of thermodynamics, which states "In any cyclic process, the entropy (disorder) must either increase or remain the same".
| 1. | When an air molecule in compartment A moving faster than average approaches the daemon, it opens the door, allowing the molecule to move from compartment A, into compartment B. |
| 2. | When an air molecule in compartment B moving slower than average approaches the daemon, it opens the door, allowing the molecule to move from compartment B, into compartment A. |
| 3. | At all other times, the daemon keeps the door closed. |
Over time, compartment B will accumulate a majority of fast moving air molecules, and compartment A will accumulate a majority of slow moving air molecules. In thermodynamic terms, compartment B will become hotter, and compartment A will become colder. In other words, through the actions of the daemon, a temperature difference will arise, where none existed before. It would seem that Maxwell's daemon has just broken the second law of thermodynamics, which states "In any cyclic process, the entropy (disorder) must either increase or remain the same".
1.1.4
Scientists, Experiments, Laws, and Theories:
Newton's _____ of gravitation. Einstein's ______ of relativity. Fill in the blanks please. According to Google, there are 34,900 web pages listed for "Newton's law" of gravity, and 7,580 web pages listed for "Newton's theory" of gravity. Again, according to Google, there are 44,300 web pages listed for "Einstein's theory" of relativity, and only 869 web pages listed for "Einstein's law" of relativity. Why is it "Newton's Law", but "Einstein's Theory"? Is Newton's law any more valid than Einstein's theory? Just the opposite is true. Einstein's theory of relativity is a more accurate description of physical reality, than Newton's so called law of gravity. The dichotomy arises because humans have a built in bias or predisposition as to what they expect, based on their past experience. What Newton described is what most humans experience AS reality. What Einstein described is counter intuitive, and NOT at all what most humans experience AS reality. Scientists being human, are also subject to predisposition in their outlook. A classic example is the Michelson-Morley aether drift experiments of the early 20th century. The experiments were conducted many times, over a number of years, using ever more complex apparatus, always with a negative outcome, until Michelson & Morley were finally forced to the conclusion that aether drift did not exist. A result in direct contradiction to what they expected, and what was widely believed by most scientists of the time. In many respects, the controversy surrounding the so called second law of thermodynamics parallels the aether drift, in that a majority of contemporary scientists believe it to be absolute, and therefore unbreakable. The simple truth is that ALL scientific principals are theories, NOT laws, and therefore subject to revision at any time, based solely on experimental results.
1.2.1
Harnessing the Daemon:
In the 19th century world of James C. Maxwell, a daemon was the only imaginable entity capable of the feats he envisioned. Today, at the dawn of the 21st century, most people own coffee pots and alarm clocks with more innate intelligence than Maxwell's Daemon. Further, most industrialized nations have manufacturing facilities capable of fabricating devices on a molecular scale. Can we of the 21st century build a daemon as Maxwell envisioned? Unlikely, for a whole host of reasons. However, this inability does not, in and of it self, invalidate Maxwell's hypothesis. Lets rephrase the question. Can we construct a device that will act as a one way trap door accumulator/coherer of heat (thermal energy)? The answer is a resounding YES. A laser is just such a device. A photovoltaic solar cell is another device. A laser converts incoherent (random) energy into coherent (ordered) energy, and in doing so, raises the effective temperature of the output beam well beyond even the temperature of the Sun. The mechanism that creates this daemon like energy trap door, is called a population inversion, and will be discussed at length in the second part of this paper. Next, consider a photovoltaic cell. It converts Sun light (disordered energy) directly into a flow of electric current (ordered energy). Again, a daemon like one way energy trap door is involved in the conversion process. A photovoltaic cell is nothing more than a solid state rectifier (generally made of silicon) that has been optimized to collect light. ALL solid state rectifiers will, to varying degrees, cohere both light and heat. In the case of heat, the phenomena is called thermal carrier injection or thermal tunneling, and results in what is known as shot noise. In most applications, this phenomena is considered detrimental, and is minimized by device design.
1.2.2
The Anti-Daemonic Rebuttal:
Those that would argue against the existence of Maxwell's Daemon will be quick to point out that examples cited in 1.2.1 while appearing to break the second law locally, do indeed obey the law globally. They will say yes, entropy is lowered locally by the photovoltaic cell, but this is more than offset by the increase of entropy in the Sun, created by nuclear fusion. In other words, they would redraw the boundary of the experiment to include the Sun, thereby avoiding any paradox between their view point and the experimental result. In the case of the laser, a similar redrawing of the boundary to include the power plant supplying the laser alleviates the paradox. All fine and good, however… Why not adopt the same redefinition of boundary with respect to Maxwell's original daemon hypothesis? Where did the kinetic (thermal) energy of the air molecules residing in the container (1.1.3) come from in the first place, if not from the Sun? Is this reluctance to acknowledge the existence of Maxwell's Daemon, another example of scientific predisposition? (1.1.4)
1.2.3
Conclusions:
That working examples of anti-entropic devices already exist (1.2.1). That these devices make use of natural or engineered "trap door" phenomena identical in concept to Maxwell's original daemon hypothesis (1.1.3 & 1.2.1). That any anti-entropic device may be made fully compliant with the second law (theory) of thermodynamics by the simple expedient of redefining the experiment boundary (1.2.2). That scientists, being human, are subject to the same predispositions of view point as any other human (1.1.4). There are NO scientific laws, only theories to which, an experimental counter example, has yet to be discovered (1.1.4).
Magneto Thermodynamics, Part 2
|
2.1.1
Introduction:
In part 1 one we covered the scientific and societal controversy surrounding Maxwell's daemon, and briefly touched on two devices that exhibit anti-entropic behavior. In part 2 we shall take an in-depth look at the mechanism responsible for anti-entropic behavior in the laser. This mechanism is called a population inversion, and until the mid twentieth century, was considered little more than a quaint mathematical curiosity, with no basis in physical reality. In order to lay a proper foundation for discussion of inverted populations, sections 2.1.2 and 2.1.3 are included as a short review of classical thermodynamics.
2.1.2
Degrees of Freedom:
At it's most basic level, the science of thermodynamics is a statistical study of vibration and movement in populations of atoms or molecules. In order to numerically quantify a population, it is necessary to understand how many different ways or modes of vibration and/or movement are available to the population. For instance, a population of molecules that have magnetic properties, when under the influence of a magnetic field, may be constrained to movement in a single direction, and yet in the absence of a magnetic field, this same population may have nearly unlimited directions of movement. In thermodynamics we use the term "degrees of freedom" to describe the number of available modes of vibration and/or directions of movement. Alternately, degrees of freedom can be viewed as the set of locations available to a population of atoms or molecules when it moves or vibrates. This set of available locations is called the population's "phase space".
2.1.3:
Temperature, energy, and entropy:
The concept of temperature arose from a need to quantify the human perception of hot and cold. However at the beginning of the 19th century, no scientist was sure what temperature was really measuring. It was well known that expending energy (doing work), such as drilling a hole, or bending sheet metal caused the material to get hot, so heat was related to energy in some manner. But what was heat? Some believed it was a discrete substance, separate from matter (they called it caloric), while others believed it was an inherent property of matter, like mass or volume. In 1877, the debate was settled by the mathematician Ludwig Boltzmann. He showed that heat is a property of matter, directly related to the energy stored in it's vibration and/or movement, AND related to the entropy (disorder) of that vibration or movement. Unfortunately his theories were met with extreme skepticism by the scientific community of that era (Maxwell was an exception). Despondent, he later committed suicide. Had he lived just a few more years, Boltzmann would have seen his theories vindicated beyond his wildest dreams. Scientific luminaries such as Albert Einstein and Max Planck used Boltzmann's theories in their work. Work that has shaped modern quantum physics as we know it today.
Boltzmann's controversial equation, Eq. 1 relates the entropy of an atomic or molecular population to it's phase space (disorder). As a side note, this equation was engraved on his tombstone...
[Eq. 1] S = k Log W
Where:
S
|
= Entropy (disorder).
|
k
|
= Boltzmann's constant (1.38 x 10-23 joules per degree Kelvin)
|
W
|
= Number of occupied locations in phase space.
|
Log
|
= Natural logarithm.
|
Form our perspective, the utility of Eq. 1 is that it defines entropy (disorder) as the ratio of energy to temperature. Looked at another way, given a population with a constant energy content, as entropy declines, temperature rises. In other words, as the degrees of freedom available to a population diminish, those few degrees of freedom still available, MUST contain the entire energy content of the population, and this causes the temperature of the population to rise.
Thanks to the genius of Boltzmann, we can define the relationships between temperature, energy, and entropy
as:
Where:
|
S
|
= Entropy (disorder).
|
Q
|
= Energy in Joules.
|
T
|
= Absolute temperature in degrees Kelvin
|
One last observation is relevant before moving on. Eq. 2b implies that for any population with a non-zero energy content, as entropy approaches zero (one degree of freedom), the temperature of the population approaches infinity.
2.1.4
Maximum disorder:
Is there an upper limit to disorder? The answer to this question depends on the degrees of freedom available to a population of atoms or molecules. For most populations, and in the most general sense of the question, the answer is "no". This answer has a practical consequence. It implies there is no upper limit to temperature, since there will always be another dimension in phase space (degree of freedom), to which we can add another increment of energy, and thereby raise the temperature of the population.
However, if a population has a limited set of dimensions in phase space (limited degrees of freedom), there is a definite upper limit to disorder. Surprisingly, the limit will be reached when exactly half of the dimensions in phase space are occupied by the population. It is obvious that when a population of atoms or molecules contain no energy, they do not vibrate or move, and therefore all members of the population occupy a single point in phase space (no disorder). Now consider the opposite condition. I.E. Every member of the population is vibrating or moving in every available degree of freedom (all dimensions of phase space are occupied). Again, all members of the population are exactly alike, and again there is no disorder. Therefore maximum disorder (and entropy) is achieved when exactly 50% of the dimensions in phase space are occupied. As a consequence of this remarkable situation Eq. 2b implies the temperature of a population at maximum disorder is infinite, and the temperature of any population where more than 50% of phase space is occupied is negative AND hotter than infinity. Figure 1 shows the relationship between temperature and phase space occupancy for a population with limited degrees of freedom.
Figure 1 - Temperature versus phase space occupancy
2.2.1
Quantum populations:
While classical physics allows populations of atoms or molecules to have nearly unlimited modes of vibration and movement (with corresponding degrees of freedom), quantum electrodynamics is a different story altogether. Consider the electron orbits of a Hydrogen atom. The allowed orbital values are discreet, and defined by Eq. 3. Therefore electron orbits represent a population with very limited degrees of freedom (dimensions in phase
space).
Where:
|
As a consequence of Eq. 3, an atom will only absorb (or emit) electromagnetic energy at those frequencies corresponding to the difference in energy between allowed orbits. In a population of Hydrogen atoms at room temperature, the vast majority of electrons are in the orbit N = 1, and the effective temperature of the orbital population is very close to zero. Now suppose we pass a controlled electric current through the Hydrogen atoms, thereby raising the majority of electrons into the orbit N = 2. We now have a population with only 2 degrees of freedom (two dimensional phase space) N = 1, and N = 2. Further, since the majority of electrons (greater than 50%) are in the orbit N = 2, the population of electron orbits is at a negative temperature (see figure 1 above), and therefore hotter than infinity. In thermodynamics terms, this is known as a population inversion, and under the rules of classical thermodynamics, was considered a physical impossibility...
2.2.2
The Laser:
In 1960, based on the thermodynamic principal of population inversion, Theodore Maiman invented the laser (U.S. Pat 3,353,115). An intense source of light or electric current is used to excite electron orbits into a population inversion. The only way these electrons can cool down is to emit a beam of electromagnetic energy (photons) at a single wavelength, equal to the energy difference between electron orbits (2.2.1). Since the population of photons in the laser beam is of one wavelength (monochromatic), they have exactly one degree of freedom, and as shown in (2.1.3), for any non-zero energy, when S = 0 (W = 1 in Eq. 1), T is infinite.
The laser uses the population inversion of electron orbits as a "daemon-like, trap door" to convert low temperature energy into a coherent beam of light, hot enough to burn a hole through the Sun
2.2.3
The second law:
The second law of thermodynamics states that:
"In any cyclic process, the entropy must either increase or remain the same".
Consider a steam engine. Steam engines can not convert all of the energy contained in the boiler to useful work. Some of the energy must be dumped into a condenser. The reason for this prerequisite is that extracting energy from a boiler lowers the entropy of the boiler, however dumping a smaller quantity of energy into a condenser (at a lower temperature) raises the entropy of the condenser more than entropy was lowered by extracting the larger quantity of energy from the boiler (2.1.3, Eq. 2a). In other words, a condenser is needed to meet the requirements of the second law of thermodynamics.
For steam engines, or any other engine that operates on the principal of heat extraction, the second law of thermodynamics IS absolute (much to the benefit of OPEC). If steam engines could break the second law of thermodynamics, then a steam engine could convert all of the energy from a boiler operating at room temperature, without needing a lower temperature condenser to dump waste energy.
2.2.4
Inverted populations:
Consider an engine extracting energy from a boiler containing an inverted population of atoms or molecules. Since the act of energy extraction, raises the entropy of the boiler (2.1.4, 2.2.1), this engine DOES NOT require a condenser, and this engine will convert ALL of the extracted energy into useful work. In other words, ANY boiler operating on the right hand side of figure 1 (beyond 50% phase space occupancy), is also operating beyond the point of maximum entropy (disorder), and unlike a conventional boiler, entropy increases as energy is extracted from an inverted population boiler. Therefore no other step is required to meet the condition imposed by the second law.
We have just uncovered a loop hole in the second law of thermodynamics. This loop hole does NOT allow us to break the second law of thermodynamics. Rather, the loop hole allows us to neatly "side step" the consequences of the second law, as it's traditionally understood to apply, with respect to heat driven engines. In other words, an inverted population exhibits anti-entropic behavior.
Or in more poetic terms, when operating on an inverted population, the spirit of Maxwell's daemon LIVES!
2.3.1
Conclusions:
That inverted populations can be created (2.1.4, 2.2.1, 2.2.2). That inverted populations exhibit anti-entropic behavior (2.2.4). That inverted populations can be used to side step certain consequences of the second law of thermodynamics as it applies to heat driven engines (2.1.3, 2.1.4, 2.2.1, 2.2.2, 2.2.3, 2.2.4). That when operating on an inverted population, the second law of thermodynamics DOES NOT preclude the existence of daemon-like "trap door" structures, as first envisioned by Maxwell (2.1.4, 2.2.1, 2.2.2, 2.2.4). In summary, some scientists will claim that while my arguments are theoretically correct, they have no basis in physical reality. I would invite these scientists to aim a high power laser at their head, then carefully examine the "theoretical hole" in their head.
Magneto Thermodynamics, Part 3
|
3.1.1
Introduction:
In part 3 of this paper, we shall examine population inversions as they apply to electromagnets. In particular, we shall discover that when viewed from the perspective of inverted populations, many devices reported as exhibiting phenomena or behavior, inconsistent with the second law of thermodynamics, are in fact, fully compliant with the second law of thermodynamics.
3.1.2
Paramagnetic materials:
Any material with un-paired electron spins will exhibit magnetic properties to a greater or lesser extent. These un-paired electrons will spin align with the applied magnetic field. In paramagnetic materials, the spin alignment disappears when the magnetic field is removed. Materials that are easily polarized produce a greater paramagnetic response. In thermodynamic terms, the paramagnetic properties of un-paired electrons represent separate degrees of freedom (dimensions in phase space) in addition to the normal degrees of freedom (vibration and movement) possessed by all materials.
Further, unlike atomic or molecular vibration/movement which exhibit strong coupling between dimensions in phase space (degrees of freedom), electron spin alignment is (in most cases) only weakly coupled to other dimensions of phase space. For this reason, it is appropriate to consider paramagnetic materials as consisting of two separate populations (electron spins, and bulk vibration/movement) interconnected through a large thermal resistance. Therefore, in many situations, each population will posses separate numerical values for entropy, energy, and temperature.
In the presence of a magnetic field, the rules of quantum electrodynamics require the un-paired electron spins be either aligned, or anti-aligned to the magnetic field vector (two dimensions in phase space). Therefore, un-paired electron spins in paramagnetic materials represent an excellent material for constructing an inverted population boiler (2.1.4, 2.2.1, 2.2.4).
3.1.3
Paramagnetic temperature dependence:
In 1880's, Pierre Curie (husband of Madam Curie), discovered the effect of temperature on paramagnetic materials, known as Curie's law Eq. 4.
It was later shown that Curie's law is just a special case of the more general Curie-Weiss law Eq 5.
Where:
Simply stated, above the Curie transition temperature, paramagnetic polarization varies as the inverse of temperature. However, at the Curie transition temperature, electron spin coupling forces cause the magnetic susceptibility to become infinite. Below the Curie transition temperature, the material exhibits ferromagnetism.
|
3.1.4
The inductor:
An inductor consists of an insulated wire, wrapped around a paramagnetic material, generally called the core. Inductors exhibit the curious behavior of opposing any change in the flow of current through the insulated wire. This electrical behavior is well understood by most scientists and engineers. However, it seems that few scientists or engineers have ever bothered to consider the thermodynamic consequences of this behavior as it applies to the paramagnetic material comprising the core of the inductor. Figure 2a shows an inductor, connected to a battery, through a switch. When the switch is closed, an electric current starts to flow through the inductor, increasing linearly over time as shown in figure 2b.
Figure 2
Consider the population of un-paired electron spins in the paramagnetic core of the inductor, at the instants just before, and just after the switch is closed.
Before the switch is closed, there is no un-paired electron spin alignment, and therefore the un-paired electron spins have nearly limitless dimensions in phase space (degrees of freedom), AND the un-paired electron spin population is in thermal equilibrium with the bulk population.
After the switch is closed, phase space collapses to just 2 dimensions, because the un-paired electron spins must be either be aligned or anti-aligned to the applied magnetic field (3.1.2), AND since the paramagnetic polarization at this instant is zero (origin point in figure 2b), it follows that 50% are spin aligned, and 50% are anti-spin aligned. Therefore, the temperature of the un-paired electron spin population is infinite (2.1.4), and obviously no longer in thermal equilibrium with the bulk population (heat flows from spin population into bulk population).
Next, as the current flowing through the inductor to rises, so does the magnetic field, thereby increasing paramagnetic polarization. Anti-aligned electron spins are flipping into alignment with the magnetic field, and since entropy is declining as energy flows into the magnetic field (the battery is doing work on the inductor), Eq. 2b (part 2) implies the temperature of the electron spin population is now negative (hotter than infinity), AND declining (2.1.4 figure 1). The situation is analogous to compressing a gas, where heat flows out of the hot gas, and into the container walls, except our "magnetic gas" is an inverted population (2.2.1, 2.2.4).
3.1.5
Inductive collapse:
Referring to figures 2a, and 2b (above), when the switch is opened current flow can not cease instantly. The energy stored as un-paired electron spin alignments in the paramagnetic core must be removed (or dissipated) from the inductor before current can stop flowing. The extreme case is represented by opening the switch, thereby causing an interruption of current flow, and results in an electrical arc across the switch contacts.
Consider the population of un-paired electron spins in the paramagnetic core of the inductor at the instants just before and after the switch is opened.
Before the switch was opened, current flow was rising (the battery was doing work on the inductor), un-paired electron spin alignment was increasing, electron spin temperature was negative and declining (inverted population), and heat was flowing out of the electron spin population, and into the bulk population (3.1.3).
After the switch is opened, the inductor must now do work on the rest of the electrical circuit in order to dissipate the energy stored in the magnetic field, supported by the un-paired electron spin alignments in the paramagnetic core. However the un-paired electron spins can not spontaneously depolarize without gaining back the heat lost during alignment. And since the energy contained in the inductor is being dissipated very quickly (by the arc), heat lost during alignment must now flow back into the un-paired electron spins very quickly as well. The ONLY available avenue for the un-paired electron spin population to achieve rapid heat inflow, is for it's temperature to drop BELOW the temperature of the bulk population. The situation is analogous to the explosive decompression of a gas, except of course our "magnetic gas" is an inverted population.
3.2.1
The magneto-thermodynamic engine cycle:
The magneto-thermodynamic engine cycle consists of three steps:
1.
|
Isothermal magnetization.
|
2.
|
Adiabatic demagnetization.
|
3.
|
Thermal equalization
|
3.2.2
Theory of operation:
The magneto-thermodynamic cycle theory of operation assumes the following two conditions.
Operating Conditions
1.
|
The use of un-paired paramagnetic electron spins for the working fluid, acting in accordance with the thermodynamic principals governing inverted populations.
|
2.
|
Adiabatic demagnetization during step two, causing un-paired electron spin population (working fluid) temperature to momentarily fall below the Curie transition temperature (3.1.3), thereby allowing ferromagnetic spin coupling forces to momentarily dominate. Since these coupling forces arise as a result of interaction with the so called "zero-point" energy of electrodynamic space (see companion paper entitled Electrodynamic Space, part 1). It follows that during step two, heat inflow from the bulk population must now overcome BOTH the normal paramagnetic polarization (3.1.5), AND the zero-point driven spin coupling forces.
|
Step 1 (isothermal magnetization) shifts the un-paired electron spin population of the inductor core into an inverted population state (2.1.4, 2.2.1, 3.1.4). During this step, as un-paired electron spins align with the applied magnetic field, the entropy of the population declines, and heat flows out of the un-paired electron spin population, and into the bulk material population (3.1.2).
Step 2 (adiabatic demagnetization) causes a rapid decline in the temperature of the un-paired electron spin population (3.1.5). During this decline in temperature, the un-paired electron spin population momentarily dips below the Curie transition temperature (3.1.3), thereby causing a momentary rise in total magnetic flux as ferromagnetic spin coupling forces contribute to overall un-paired electron spin alignment. This momentary flux increase represents an additional increment of electromagnetic energy (beyond the energy stored in the inductor during step 1), available to the driven circuit. Therefore the electromagnetic energy derived from the inductor during step 2, is greater than the electromagnetic energy stored in the inductor during step 1.
Step 3 (thermal equalization) Allows sufficient time for the heat deficient (caused by step 2), to be replenished from the ambient environment.
As a practical consequence of the two conditions (listed above), the magneto-thermodynamic heat engine will operate from ambient heat sources, without requiring a lower temperature condenser to dump waste heat. In other words, the magneto-thermodynamic heat engine is a "perpetuam mobile of the second type", and satisfies ALL requirements of James C. Maxwell's Daemon, as he envisioned it.
Next, we shall cover each step in detail.
3.2.3
Step 1, Isothermal magnetization:
In figure 2a (above) the rate of change in current flow is set by the ratio of electric potential (voltage) to inductance as shown in Eq. 6.
[Eq. 6]
| 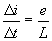 |
Where:
i
|
= Current in Amps.
|
t
|
= Time in seconds
|
e
|
= Potential in Volts
|
L
|
= Inductance in Henneries.
|
The rate of change in current flow can be made arbitrarily small, by making the ratio of electric potential to inductance small as well.
Since the degree of un-paired electron spin polarization is directly dependent on the magnitude of current flow through the inductor. It follows that a small rate of change in current flow will yield an equally small rate of change in un-paired electron spin polarization, and this will result in a small rate of heat outflow (into the bulk material population), and therefore a small temperature rise across the thermal resistance separating the un-paired electron spin population from the bulk material population (3.1.2, 3.1.4), thereby causing the smallest possible decline in magnetic susceptibility of the paramagnetic core of the inductor (3.1.3).
Strictly speaking step one is NOT isothermal. However by proper circuit design and choice of paramagnetic core material, the decline of magnetic susceptibility in the core of the inductor can be minimized, which is the ideal condition for this step.
This step represents the compression stroke of our engine.
3.2.4
Step 2, Adiabatic demagnetization:
The time required for inductive collapse is set by the ratio of inductance to driven circuit impedance as shown by Eq 7.
[Eq. 7]
| 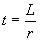 |
Where:
t
|
= Time in seconds.
|
L
|
= Inductance in Henneries.
|
r
|
= Driven circuit impedance in Ohms.
|
The length of time required for inductive collapse can be made arbitrarily short, by making the driven circuit impedance very large.
The purpose of this step is to force the temperature of the un-paired electron spin population to fall below the Curie transition temperature (3.1.3, 3.1.5, 3.2.2), and thereby cause the magnetic susceptibility of the core to become infinite (onset of ferromagnetic behavior). The ideal condition is met when the rate of change in the magnetic field of the inductor never drops to zero. If the un-paired electron spin population temperature become too cold, the core will momentarily "freeze" in the ferromagnetic state, thereby causing the rate of change in the magnetic field to become zero.
During this step, the heat inflow to the un-paired electron spin population from the bulk material population is greater than the heat outflow during step 1 (3.2.3). The reason being that heat inflow must overcome both the electron spin coupling forces caused by passage through Curie transition, as well as the regular paramagnetic polarization. Conversely, the electrical energy delivered to the driven circuit by the inductor during this step, is larger than the electrical energy stored in the inductor during step 1.
In effect, step two has converted quantity of thermal energy into electrical energy.
Strictly speaking step two is NOT adiabatic. However, by proper circuit design and choice of paramagnetic core materials, the rise in magnetic susceptibility during this step can be made sufficiently large.
This step represents the power stroke of our engine.
3.2.5
Step 3, Thermal equalization:
As the name implies, the purpose of this step is to allow the electron spin population and the bulk material population to once more, achieve thermal equilibrium with the ambient environment. While in the strict sense of the magneto-thermodynamic cycle, this step is not required, it's inclusion greatly simplifies circuit design.
This step represents the intake stroke of our engine.
Further, NO exhaust stroke is required, since our engine utilizes an inverted population of un-paired electron spins, as it's "working fluid" (2.2.4).
3.3.1
Summary:
The fringes of scientific research are literally teeming with reports of inductive kickback devices that exhibit anti-entropic behavior or phenomena. Most are dismissed as the rantings of crackpots and lunatics. This paper presents a coherent rational explanation, based on proven scientific principals, in support of these devices, and the phenomena observed. It is also intended as a "how to" guide for current and future researchers in achieving optimal performance from their devices. To those free thinking individuals, operating at the boundaries of knowledge, I dedicate this paper.
3.3.2
Conclusions:
That un-paired electron spins in paramagnetic materials will exhibit the characteristics of an inverted population (3.1.4). That a population of un-paired electron spins can be made to interact with the zero point energy of electrodynamic space, thereby capturing thermal energy, and making it available for work (3.1.2, 3.1.3, 3.1.5, 3.2.2, 3.2.4). That a cyclic heat engine, based on a working fluid, utilizing an inverted population of un-paired electron spins is possible (3.2.1, 3.2.2). That said engine will exhibit anti-entropic behavior fully consistent with the principals of James C. Maxwell's Daemon (3.2.2, 3.2.4, 3.2.5). That said engine is in fact, a perpetual motion device of the second type (3.2.2, 3.2.4, 3.2.5).


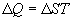
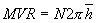
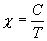
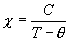
No comments:
Post a Comment